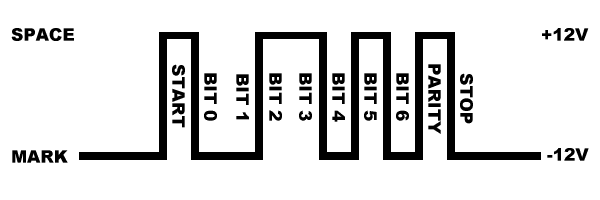
Alexander Wilson, 2014
The term “process” usually connotes continuity. The canonical heraclitean river, different each time one enters it, presents the essential character of process: it flows. Digital processes, however, are characterized by cuts, breaks, and jumps. The digital is given as a series of discontinuities. We look at the river flowing: it seems continuous, a unified flux. It is highly entropic, meaning it exceeds our capacity to resolve the minuscule details we assume compose it (water molecules). Every time you walk into it though, it feels decisively different. It may be warmer today than yesterday, the current might be stronger or it may have waned.
Process implies change. But change in the digital realm can only happen discretely: one moment we have one state, the next we have another. One moment the water is warm, the next it is cold. There is nothing in between. No process to speak of. In this sense the digital neatly seems to elide change. Nothing has been altered. The state space in the digital domain is finite; so it is as though the various moments in the digital process are given all at once, and for all eternity. Indeed, one might say they are “outside of time”, for these states, in themselves, are not affected by the process; they are exactly the same each time they are taken up. Process hence seems to move the digital from the outside.
The digital is inseparable from processes of “discretization”, as Bernard Stiegler observes. It is simply the process that cuts continuities into discontinuities, making unified, homogeneous mixtures discrete, nameable, mobile, functional. Stiegler usually looks at this as a (pre)historical or anthropological process (ie: grammatization). But following Simondon, it is also possible to interpret this as an ontogenetic process. Simondon envisions the evolution of technology somewhat like thermodynamic process: a crystal propagating through a supersaturated solution, where the unified mixture of molecules is progressively organized, and structured, put to the service of the reproduction of the given symmetries ad infinitum, mechanically and algorithmically, until the favorable circumstances, or preindividual potentials, are exhausted.
The digital is intimately related to such an ontogenetic process of selection. It is as though the algorithm prefigures the digital. The if-then decisional procedure of the algorithm gives rise to the series of cuts typical of the digital process, as the ebbs and flows of the unidentified, unresolved chaos “outside” is sampled, once a threshold of potential is met. Snapshot. The digital emerges in the moment of sampling; it is in the only moment a determinate system touches an indeterminate, un-incorporated preindividual “outside”, that a “bit” comes into existence. Without this moment, the digital is not connected to any process: it is, like the crystal in the mind of the crystallographer, an eternal and infinite expanse of symmetries. Hence, again, the digital seems moved by processes outside of itself. The digital process, therefore, always implies the “analog”. But this crude term is hopelessly inadequate for signifying the monstrous radical contingency that hides in each sampled interval, in between the quantized cracks of our pixels and voxels.
But what is this outside? The outside, in a cybernetic sense, is simply that which interacts with a given system through its inputs and outputs. A system is said to be operationally closed implying boundaries and definite topological connectivity. It will typically be composed of various (continuous) flows, feeding back upon themselves, according to a certain topological arrangement, implying certain thresholds, minima and maxima, varying ebbs of potential. The feedback loops themselves imply recursive processes. For digital cuts to emerge, loops in the process are necessary. The digital bit is born out of a specific decision implied by the structural coupling of some chaotic outside with some defined inside: physicists will call this measurement or observation.
In order for a proper “digital process” to be conceived as a series of cuts, these cuts and breaks have to be recorded or inscribed in some context. The system must somehow change to receive the event. If it does not change, then nothing has happened. As people say when someone makes an unbelievable claim: “picture, or it didn’t happen”. Indeed, nothing happens that is not somewhere inscribed in some context. This is Landauer’s principle: no information without implementation. For something to happen, it must happen to something. The very structure of information pivots on the fact that events leave a trace. To use Bateson’s adage, events make a “difference that makes a difference”. If the event does not get inscribed anywhere, it doesn’t make a difference to anything or for anything, and hence didn’t happen.
It is important to underline that even mathematics is plagued by a fundamental randomness. Chaitin’s famous “Omega” exemplifies this. It distributes all possible decidable and undecidable computations in an algorithmically random manner. And it would seem that in cosmological physics, too, with the advent of the holographic principle, the “observable universe” much like the projection of a hologram, emerges from a discrete two-dimensional set of randomly distributed bits at the Planck scale, corresponding to the surface of the initial inflationary break from symmetry which gave rise to “everything”. Here “everything” should remain in scare quotes, because scientists will disagree as to whether this non-pattern truly does imply totality. Like the “thumbprint of god” (a term once used to describe Mandelbrot’s fractal), the digital in its extremes seems to encounter an absolute contingency “outside of itself”. The “observable universe” is bounded by pure ungrounded randomness; and all process is a coupling of this randomness and some procedure for resolving it. The absolute outside implies the symmetry of pure randomness. And randomness is dialectically opposed to the asymmetry of the observer and the event observed. Similarly, the digital always already implies the procedural abstraction, the algorithm, that leads to its sampling and resolving.
Whether it be the decisive moment of a discerning subjective judgment, or the quantized capture of an electronic converter, the discrete’s process is extrinsic to it. Contingency is not digital. Change is not digital. Process is absolute difference; it shuffles things around when you’re not looking, not selecting, not judging, so that the next time you peak something has changed. Difference, in itself, does not (yet) “make” a difference. It “makes” a difference in the moment of the break, the rerouting of the topology of the circuit, when it inscribes the event into some context: an intensity is measured, an aesthetic is judged, a value is attributed, a signal is sampled.
It seems to me the movement from the “prediscrete world”–that of our archaic ancestors, for example, who did not have a word for each object around them–to the grammatized world, can be modeled in the fashion of the process leading through a simple analog-digital converter, where a continuous (unified) flow is sampled and transformed into a series of discontinuities. Discretization opens up new possibilities; these are related to the “mobility” afforded to the discrete. The atomists believed that the void, the space between atoms, explained movement. In much the same way, the breaks between the discrete bits of the digital, allow them to become mobile within their space of possibility in a way a continuous flux simply cannot. Digital information can be copied precisely, whereas analog information can only be copied at a loss. These abilities stem from the following fact: as “individualized” objects, bits are disconnected from their surroundings, they are mobile. I say “individualized” to reiterate that, following Simondon, this is a state which no longer harbors any intrinsic potential, for it comes at the term of a process which has exhausted its “preindividuality”. Its potential to become, to change, for Simondon, is predicated on this preindividuality. Thus there is a sense in which, once an object is perfectly objectified, that is, once it can be specified (copied) with absolute precision (as with a collection of digital bits), it does not contain within itself the capacities of process, change, becoming. Hence, any process of such objects to speak of must originate outside such objects.
This again implies that process is something distinct from the digital. When we have digital bits, or when we have purely defined objects, we still don’t have an account of change or time. This is a big problem with object oriented ontology, for example. It is also related to what Quentin Meillassoux describes as hyperchaos: interestingly, he arrives at the conclusion that contingency (ungrounded, unmotivated, indeterminate change) is necessary, because of the non-totalizability of the cosmos (the whole), as per the paradoxes of set theory. If the cosmos itself cannot “contain” itself, or if there can be no absolute whole of everything, he reasons, then we must posit the necessity a kind of ungrounded change that escapes the determination of any holistic set of possibilities or laws.
In Deleuze there is further support for this idea. Pure difference, difference in itself, is a positive concept for Deleuze; it is not subordinated to representation, identity, negation, and basically all the features required for the digital domain’s ability to be specified to absolute precision (or precisely copied). At issue is more than just a relation between digital and analog or discrete and continuous. The pivotal relation is rather between “difference” and “difference that makes a difference”. In Deleuze, difference is never given; rather, it is that which gives the given. Difference has an ontological necessity to give us discrepancies and identifiable distinctions. What is given is discrepancies, distinctions, relations of identity and contiguity: what we generally will call “information”. Deleuze insists that as things individuate, difference never gets “used up”. Only diversity, he says, is truly reduced in the processes. Difference stays intact, he insists, surviving all possible transformations. Process, change, time, stem from what we might call the “ontological incontinence”, a fundamental unrest of difference in itself, that is, before it gives the given or “makes a difference”. This is also related to his concept of “quasi-causality”, which conditions events through “surface effects”, yet, which is “unproductive” in a way amenable to how difference does not get used up in causal process. Notably, he claims, after Valery, that the deepest level of being is the skin, implying that such surface effects, which are “causally unproductive” are that which give us causal relations in the first place.
Which brings me to my point about Chaitin’s Omega. Omega is really a formal mathematical object, constructed in order to show the “probability” that a given program of N bits is decidable or undecidable. This is in the spirit of Turing and the decision problem, formulated as a question of whether a device churning through a computation would ever come to halt on a definitive “yes or no” result. We know since Gödel that mathematical systems are “incomplete”, because they allow expressions that are consistent yet cannot be proved. This responded to Hilbert’s first and second questions: mathematics is incomplete if consistent. Hilbert’s third question remained: is mathematics decidable? Turing’s machine was a thought experiment for responding to this. (It is very telling that his thought experiment actually paved the way for modern computing: the “general purpose computer”, is what is mathematically called “Turing Universal”). As it turns out, using a technique similar to Gödel, but inscribed into the procedure of the machine, he showed that the decision problem is unsolvable, that is, there is no algorithm or shortcut procedure for knowing in advance whether a certain computation will halt, or whether it will keep on computing forever, alternating eternally between true and false, following the liar’s paradox. Chaitin sees this as fundamental, and extends it with Omega: what is the probability that a given program will halt? It turns out that this number, for programs of any arbitrary length, is a seemingly infinite and random stream of digits: even if you knew the number to the Nth placeholder, you would still have no way of deducing what the next digit would be. It has maximal “algorithmic information content”: each number in the probability is a singular, irreducible event, which is “independent” in the mathematical sense, uncorrelated to the other numbers in the sequence. The probability of a given computation being decidable is thus random in this sense.
To return to our “thumbprint of god” analogy, it is as though, not only physics, but also mathematics, is undergirded by a fundamental randomness. I see this as equivalent to Deleuze’s idea of quasi-causality: it is this unproductive conditioning of everything, from an absolute ungrounded difference outside of the system. It seems everywhere we dig, we are confronted with this randomness. Chaitin notes that this denies Leibniz’s principle of sufficient reason and ultimately limits the purview of Occam’s razor. Yet in another sense I think it gives substance to Leibniz’s cosmological argument. But we should change his question from “Why is there something rather than nothing?” to “why is there non-randomness rather than randomness?, or “why is it there seems to be stability, locality, law-like repeatability, rather than absolute contingency all the time?”. I think it has something to do with observation itself. Randomness is that which requires no explanation. No one ever looks at a randomly distributed array of objects and asks: why are these objects randomly distributed? What requires explanation is that which diverges from randomness, because statistically, a non-random distribution is less probable than a random one. We are very good at identifying patterns. Humans, and indeed living organisms generally, are pattern recognition systems. In fact we are so good at it that we see patterns (coincidence) even when things are random (see Kahneman and Tversky). As we sample the “chaotic outside”, as we cut off a bit from its preindividuality, and endow it with mobility and nameability, it becomes a determinant in time, an anchor, an irreversible fact, a point of equivalence between potential and actual, and is encoded in our very structure as pattern-recognizing agents. In quantum physics, this will be called the “collapse” of the wave function, or better, “decoherence” (check out Zurek’s work), in which the observer, the act of measurement, or the event of interaction is central to the transition from randomness and non-locality to predictability and locality. Observation causes a bias on reality: a “predictability sieve” as Zurek calls it. Once a particle is “entangled” with another, their futures are interdependent and correlated. On the quantum level a thing is here AND there at the same time. In the classical level of reality (where we carry out our lives), a thing is here OR there. Decoherence is the transition from the “and and and…” to the “or or or…”. Similarly, irreversibility and process emerges in the moment we measure. The event is the Aion: it cuts the reversibility of the Chronos and gives us the irreversibility of the before and after. As in Hölderlin’s caesura, the beginning and end no longer rhyme. The “and and and” is difference in itself. The “or or or” is difference that makes a difference for something or someone.
To me all this suggests that process is necessarily “outside” the category of the digital.